When I was in high school, I would solve problems in math class, wondering when I would ever need to do this in life. Naturally, I was wondering the same thing when I was studying algorithms and data structures.
But my math teacher’s words stuck with me - “you might need it only once, but you’d be better off knowing it”.
So through grinding teeth, I studied the computer science theory that I found so boring at the time. Each time my attention shifted I remembered her words and traversed yet another tree.
Six years later, my team got ownership of a microservice that would serve as a task engine. Upon receiving a request, it executes several tasks and each one could depend on any number of others before it.
For example, one of them retrieves the authenticated user’s details. There could be a lot of other tasks that need to access the user’s information to complete, so they need to wait for it to complete first.
The tasks are not in a fixed order, so depending on the request we may need to execute only a fraction of them. But they still need to maintain that dependency order, so hardcoding the execution paths was not possible.
To make things even more interesting, each request had a certain time limit in which it needs to complete all tasks. If the time ends before all tasks have finished, then we should return the results of those that have been completed and cancel the rest.
Dissecting the Problem
When faced with such a complex problem I first try to ignore all business-specific details and lingo. Instead, I brainstorm on an abstract level to understand what the challenge is. I want to come up with a couple of ideas and make a stab at the problem.
Each task represents a function. We have a set of functions that need to be executed in a specific order. They need to be able to pass data between each other. We need to be able to run the functions without dependencies concurrently to save time.
First I had to figure out in what data structure I could keep the tasks and how I could pass data between them.
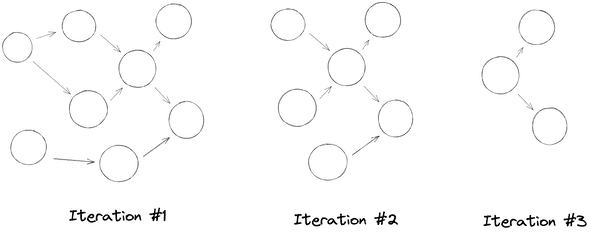
I remembered an article about Webpack that I read some time ago. It described how Webpack resolves imports by building a dependency graph. On a conceptual level, this seemed similar. I could build an acyclic directed graph where each node would resemble one of the tasks and the edges would be the dependencies.
Resolving the tasks would mean traversing the graph in the order of dependencies. The first algorithm I wrote looked for all nodes without edges pointed to them and resolve them. Then repeat that until there are no nodes left in the graph.
The data sharing could be solved by a context object. They could all get passed a reference to a global object they can read and update data in. The implementation was in Node, so access to the context would be memory-safe.
// Register each task in a central place to avoid errors
enum TaskName { ... }
// Holds data passed between all the tasks
interface Context { ... }
// Each task must return a specific structure
interface Result { ... }
interface Task {
name: TaskName;
dependencies: TaskName[];
run: (ctx: Context) => Promise<Result>
}This is how we implemented the tasks. Each one had to provide only the bare minimum - its name, the list of tasks it depends on and the function it executes. It doesn’t have to provide the dependencies in order since we construct the graph dynamically.
The Flaw
I was confident in the implementation and I was happy that I found an application for my graph traversal knowledge. But it had a massive flaw that I had somehow overlooked. It was caught in code review and I felt quite uncomfortable for not thinking of it sooner.
This graph resolution will move with the speed of the slowest task on each cycle. If speed wasn’t important that would have been fine. But we want to make sure that we resolve as many tasks as possible because each run is racing against time.
Implementing it this way meant that some tasks could be run concurrently would have to wait. Two execution paths that have the same number of nodes would have to wait for the slower ones to complete at each cycle. That way one path through the graph that took less time would still be completed with the speed of the slowest path with the same number of nodes.
The Second Design
It was a tough situation staring at something I had put so much thought into, knowing that it doesn’t fit the bill. I wasn’t sure whether I could make it work with the implementation I had. I didn’t even know where to start and whether I could figure out the algorithm on my own.
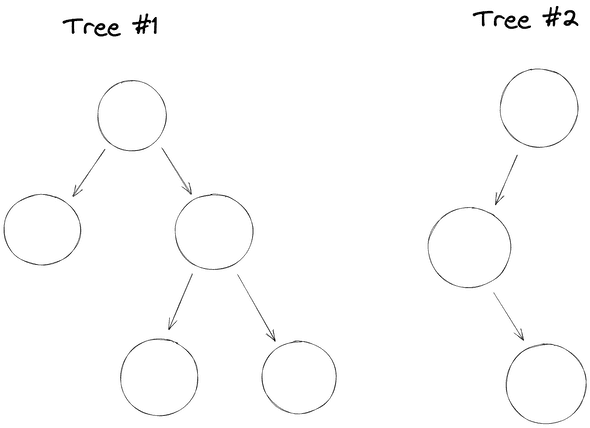
Then a colleague proposed splitting each execution flow into its own data structure so they can be traversed in parallel. Instead of graphs we created a tree for each task without dependencies and placed it at the root. We could traverse them independently.
That solved the speed problem but introduced a new one. In the graph, multiple tasks could depend on another one. When we have different data structures we will have to resolve the same task twice in each one. This is something we couldn’t do because of the tight performance requirements.
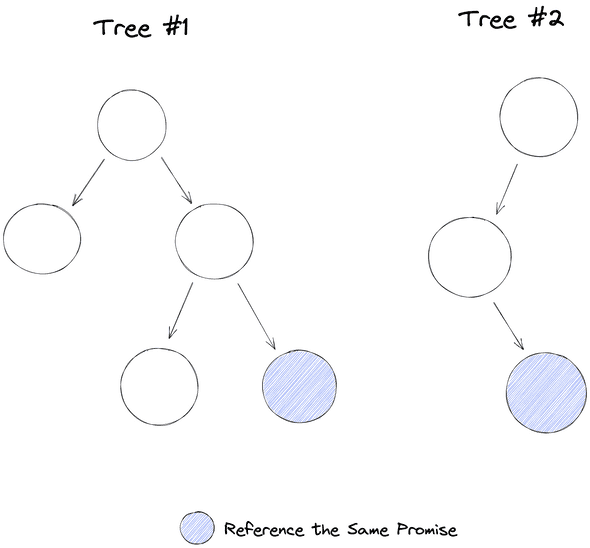
So we took advantage of a core JavaScript feature. Each task function returned a promise because it was async. The key thing about promises is that they resolve only once. Once they are resolved they hold their value and they can provide it immediately.
So we solved the problem by keeping a reference to the same promise in each tree. That way once the promise is resolved in one of them, the next task that needs it will have the value ready even though it’s in a different data structure. It removes the problem with race conditions and multiple requests because the promise remains pending until it resolves.
Lessons Learned
I’ve heard the phrase that the first implementation is always a prototype so many times. Yet, I often commit to the first design I can think of, losing the ability to see beyond it. If I had drawn the graph solution on a piece of paper I would’ve saved a few days of work, knowing that it won’t solve the problem.
Now whenever I’m working on something more complex, I ask myself how would I solve this problem if my first idea wasn’t an option. This forces me to think of a design from a completely different angle. Then if my initial idea still seems like the better option I can commit to developing it.